Linear Algebra as Spreadsheet
Thanks to Garth Goldwater for a lot of the ideas here
The metaphor isn't mine. But it's a good one!
Is there an intrinsic reason MATLAB-esque tasks can't be as WYSIWYG as a spreadsheet?
— Max Krieger (@maxkriegers) April 5, 2020
How do you represent matrix multiplication in a graphical environment? I want to drag and drop my eigendecomposition as tangibly as a sort operation.
Some tools on the way to supporting the magical, playful mode of waves:https://t.co/fa5Sunkwhhhttps://t.co/FQKTRWzyje
— Max Krieger (@maxkriegers) September 16, 2020
and the unimplemented direct manipulation APL-spreadsheet-incantation environment of my dreams https://t.co/TFxhVS1UIq
So I was wondering why nobody took it literally.
When you're manipulating matrices, you [often] lose track of, "what am I doing? what does this mean?" I've got this funny matrix, I multiply it by a vector, what was this supposed to do?
- Keenan Crane, Discrete Exterior Calculus
I can't find any existing direct manipulation interfaces to perform linear algebra on raw data. Stuff like eigendecomposition or factorization. Or constructing proofs of SVD.
The key, I think, is to map the language of linear algebra to an interaction semantics for linear algebra (How do you create an interaction semantics?).
Here's what I have found:
Excel!?
Sure I guess?
APL Is Really Cool
Aesthetics
other
- What if there was a set of flashcards to learn all the APL symbols? Like Elixir Cards/PixelSpirit.
One subproject (Downscoping as a skill (subprojecting)) is not APL, but some CAS matrix toy - "Linearkit".
- Nicky Case's transformation matrix toy
Direct manipulation refs
- 2d
isolate a data column by dragging it out of the table. also got a little semantic text editing going pic.twitter.com/ZW6ukuk2UK
— Paul Shen (@_paulshen) March 2, 2021
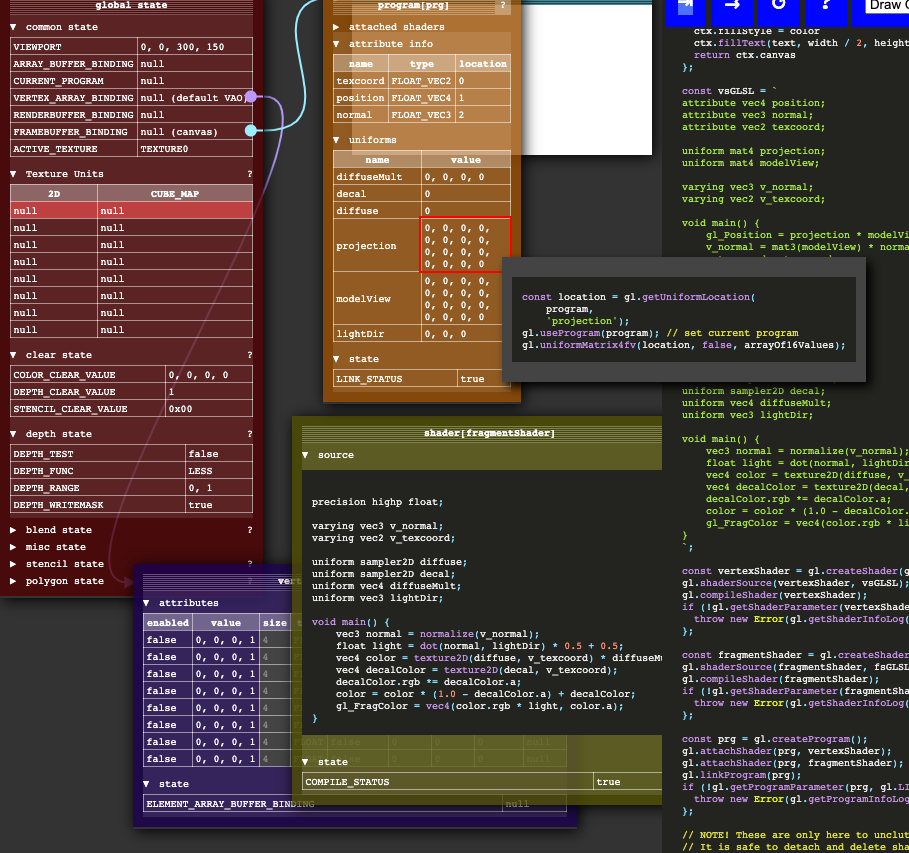
- WebGL State Diagram - the "cells" are pointers
- Maybe each matrix is a floating table and you can multiply by constructing a graph of edges?
- Graphical Linear Algebra
- Graspable Math
- Responsive Matrix Cells: A Focus+Context Approach for Multivariate Graphs
- Loglo
- Math Inspector
-
Math inspector makes it easy for anyone to leverage the power of numpy, the most popular computational mathematics library in the world, without needing to know anything about programming or writing any code. “If watching math videos is like going to the movies instead of reading a book, then math inspector is like playing a video game instead of doing your homework.”
-
- Interactivity of Visual Mathematical Representations: Factors Affecting Learning and Cognitive Processes (pdf)

Semantics refs
- Graphical Linear Algebra
- An Illustrated Guide to Arquero Verbs / UW Interactive Data Lab / Observable
- A Grammar of Data Manipulation • dplyr
- "Verb-noun vs noun-verb"
- Thoughts on how to find alternate algebra-like systems
- Named tensor notation
- https://github.com/amzn/computer-vision-basics-in-microsoft-excel
Every right click transformation (eg transpose, get eigens) is not in-place but is placed somewhere else in space, immutable copy, like Paul Shen's systems.
Applications
- Learning, proving, playing
- graphics pipelines (in 2d case of env layout)
- statistics
- DSP (vision - convolutions, audio)
- ML
Why?
- Not sure.
- Might be internalized trauma taking linear algebra without something that feels nice to use (Domain-Learning with Computational Microworlds).
- Practitioners make numpy mistakes a lot I bet
- How do you communicate intuition about powerful ideas in linalg? Are pictures the best we have? What about the algebra, and the data embedded in every matrix?
- The semantics of Linear Algebra are pretty well-defined I think? That's why it's an algebra, right?
- I want to do casual mathematics
- Linear Algebra can model a lot of other domains of math. Not to mention it's pretty useful for physics. So maybe the interface paradigm can be juiced into domain-specific applications (On Juicing, Bottom Up Design).
https://arxiv.org/abs/1702.02131
https://jhupbooks.press.jhu.edu/title/chinese-roots-linear-algebra
https://www.goodreads.com/book/show/2448489
https://github.com/Timwi/HexagonyColorer
https://cragl.cs.gmu.edu/iheartla/rethinkingpapers/preprint.pdf
https://twitter.com/anton_hilado/status/1289956291750887424?s=09
https://www.labri.fr/perso/nrougier/from-python-to-numpy/
https://github.com/rougier/numpy-100
https://rajatvd.github.io/Factor-Graphs/
https://guillaumegenthial.github.io/image-to-latex.html
Spectral clustering/decomposition of some images you drag in
Gensim
https://auto.gluon.ai/stable/index.html
https://math.mit.edu/~gs/learningfromdata/
https://twitter.com/SC_Griffith/status/1506489478453600258?s=20
Lots of matmul happening here: https://www.mattkeeter.com/projects/mrep/
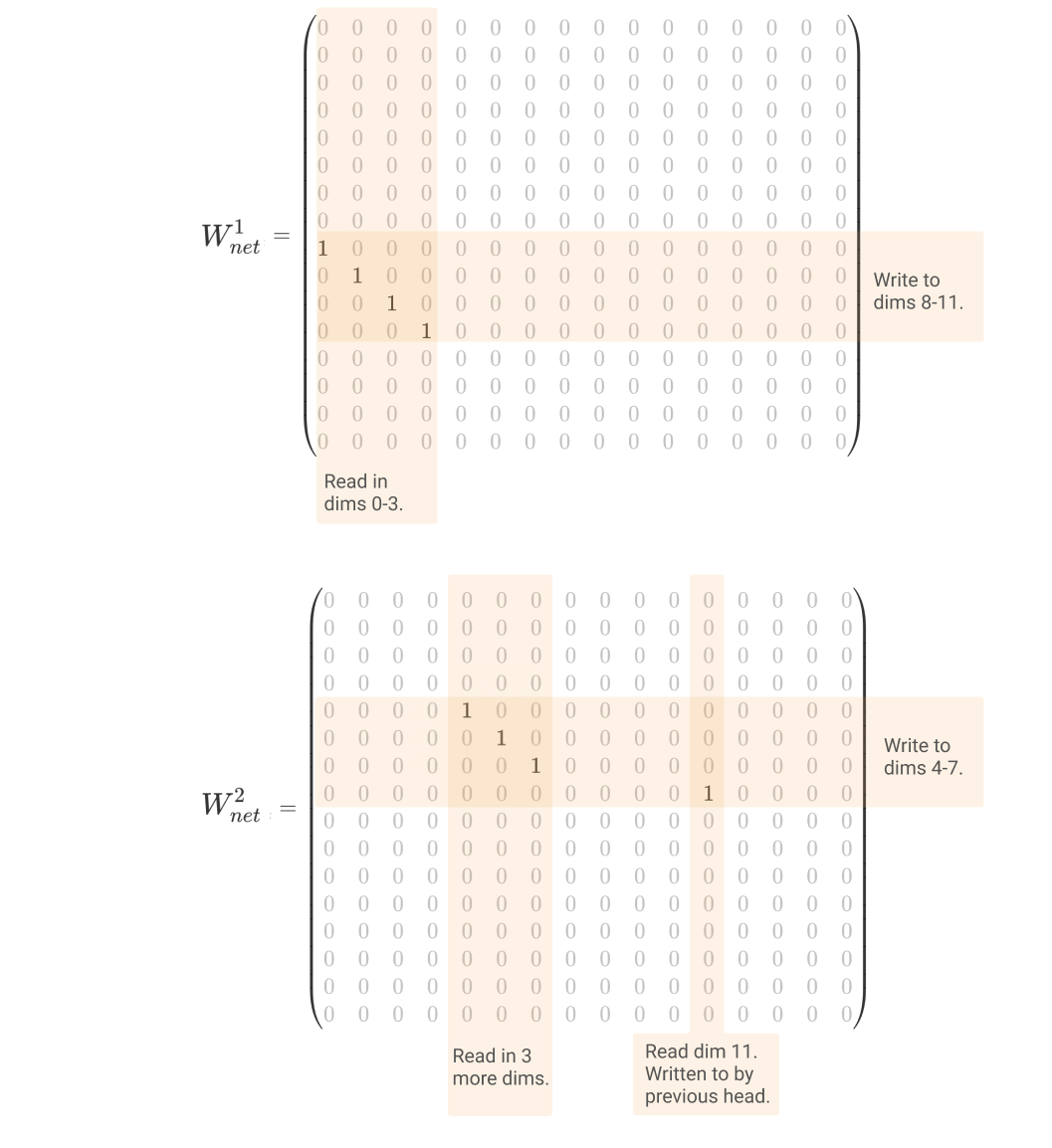
https://transformer-circuits.pub/2021/exercises/index.html
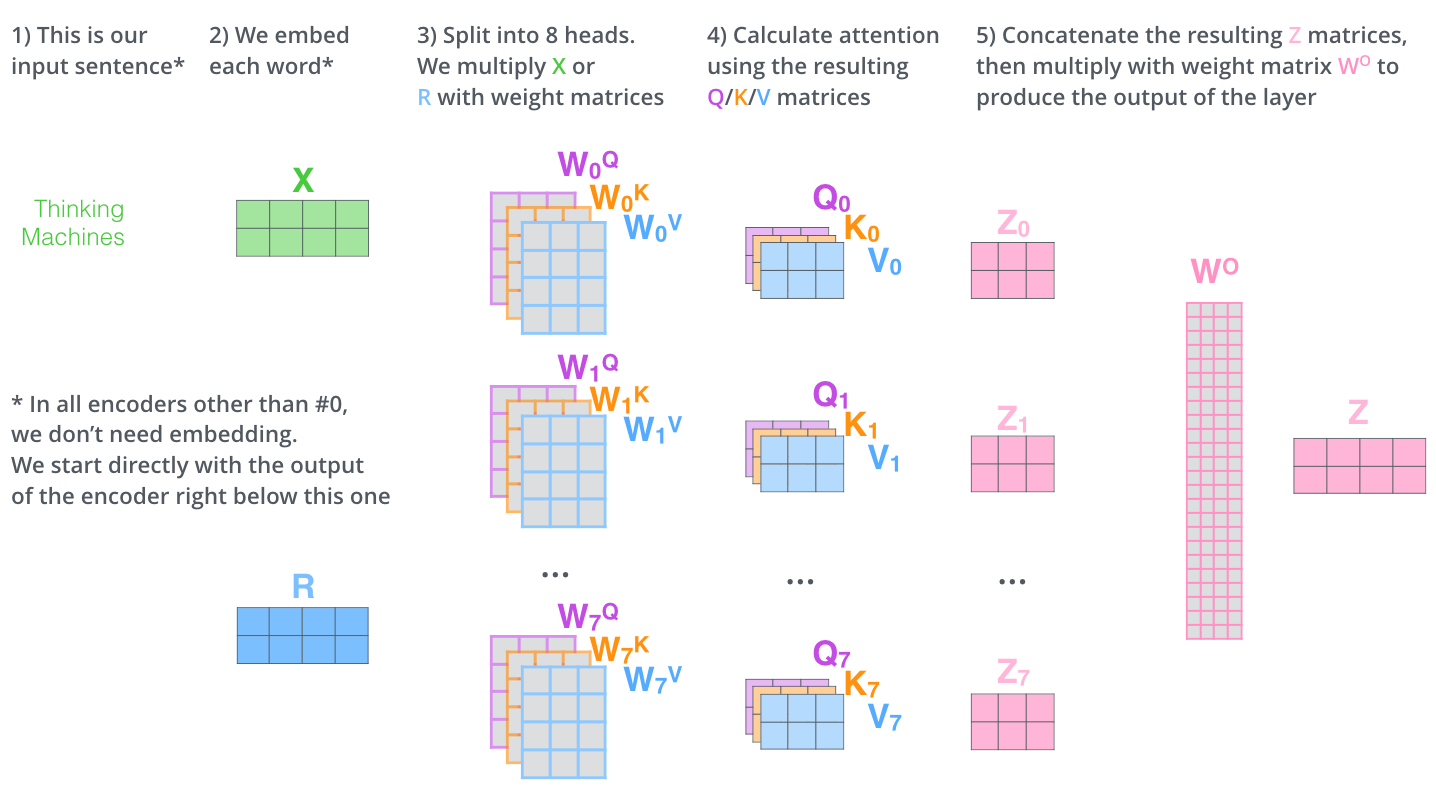
https://jalammar.github.io/illustrated-transformer/
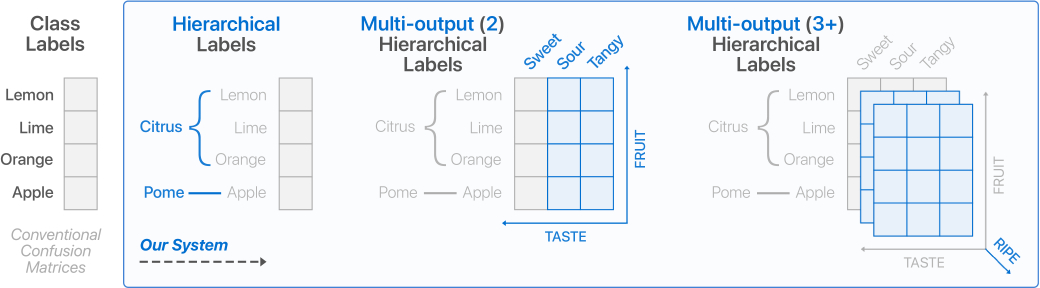
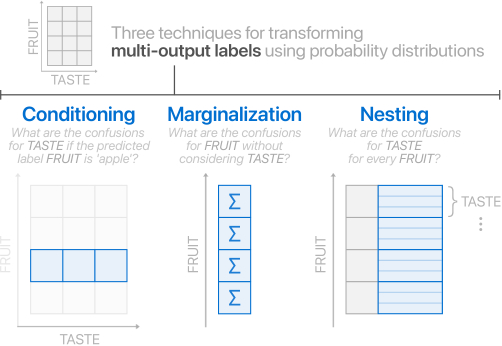
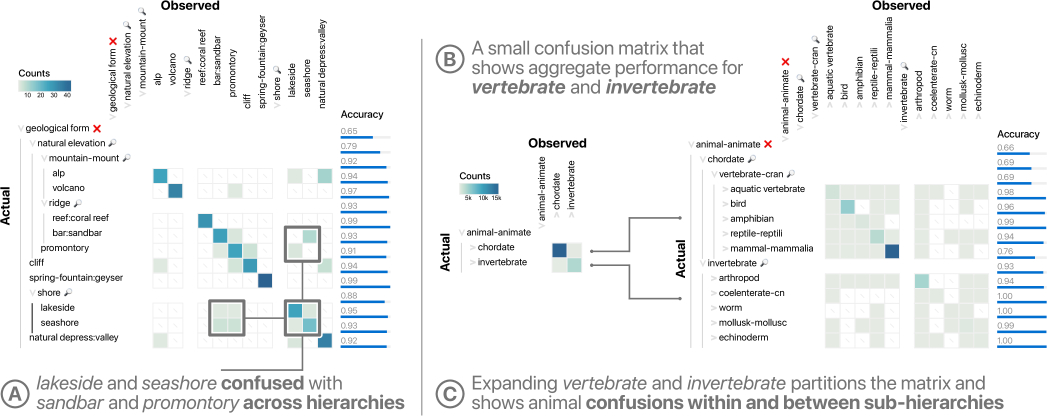
https://dl.acm.org/doi/fullHtml/10.1145/3491102.3501823
https://twitter.com/jeremyphoward/status/1523775789879422976?s=21&t=ecPZB2KLDqNU4hC58wRbmQ
https://twitter.com/mark_riedl/status/1555188022534176768
https://github.com/quil-lang/magicl/blob/master/doc/high-level.md
https://twitter.com/joel_burget/status/1562469068464017408
https://jupyter-contrib-nbextensions.readthedocs.io/en/latest/nbextensions/varInspector/README.html

https://e2eml.school/transformers.html
https://github.com/srush/Tensor-Puzzles
I should definitely do this first https://minitorch.github.io/ https://numpy.org/doc/stable/user/basics.broadcasting.html
https://github.com/kenjihiranabe/The-Art-of-Linear-Algebra
https://github.com/xl0/lovely-tensors
https://twitter.com/_paulshen/status/1600653533371863040
https://news.ycombinator.com/item?id=30101637
Linear algebra brushes https://twitter.com/Wattenberger/status/1610472915623112704?s=20&t=ATlA1Rzg3kVKSSUco2KTLw
https://www.math.uwaterloo.ca/~hwolkowi/matrixcookbook.pdf
https://x.com/voooooogel/status/1701290465482645808?s=46&t=ZaQiMOEZuQ_6mGivtLEwMA
Children
Backlinks